ChatGPT generated image
What Underfitting is and How to Test for It and Minimize its Impact
Machine learning stands as a pivotal element in contemporary data science, fundamentally altering the landscape of predictive analytics and decision-making across various domains. We have written many articles on machine learning concepts, but this one takes us back to some basics!
Despite its widespread adoption, a significant impediment exists in the form of underfitting, wherein machine learning models fail to capture the underlying patterns in training data, resulting in poor performance on both familiar and unfamiliar datasets. Underfitting not only compromises the accuracy of predictions but also limits the potential of models to learn complex relationships within data. This challenge underscores the imperative for robust techniques to address underfitting and enhance the learning capacity of machine learning algorithms across diverse scenarios. Knowing how to appropriately resolve underfitting is essential for ensuring the dependability and effectiveness of machine learning models in real-world applications spanning diverse fields.
The concept of underfitting within statistical modeling and machine learning is deeply rooted in history, evolving alongside advancements in mathematics, statistics, and computational capabilities. Although the term “underfitting” may have gained prominence more recently, its fundamental concept and consequences have long been acknowledged. The origins of underfitting can be traced back to the early stages of statistical modeling, where researchers and statisticians initially relied on overly simplistic models with limited parameters to explain complex relationships among variables. These models, while easy to interpret, often failed to capture the underlying structure of the data. As datasets grew more intricate and computational power advanced, the limitations of such simplistic approaches became increasingly apparent. This historical context highlights the persistent challenge of balancing simplicity with accuracy, emphasizing the need to develop models that are sufficiently expressive to learn meaningful patterns without being overly constrained.
Here are some concrete examples to elucidate the ramifications of underfitting. For instance, in a machine learning task centered on dog image identification, a model that relies only on very basic features — such as overall brightness — may be too simplistic to differentiate dogs from other objects, leading to poor classification performance in both indoor and outdoor scenes. Similarly, in predicting academic outcomes, a model that only uses a minimal set of features like student age or attendance rate, while ignoring critical indicators such as grades or engagement, may fail to capture the complexity of academic success. This can result in consistently inaccurate predictions across the board, regardless of the student’s background.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Simulated dataset: academic performance
# Feature: attendance rate (%), Label: final score
data = {
'attendance': [60, 70, 80, 90, 95, 100],
'study_hours': [1, 2, 4, 6, 7, 8],
'final_score': [50, 60, 70, 85, 90, 95]
}
df = pd.DataFrame(data)
# Intentionally underfit by only using attendance, ignoring study_hours
X = df[['attendance']]
y = df['final_score']
# Fit linear regression
model = LinearRegression()
model.fit(X, y)
# Predict and evaluate
predictions = model.predict(X)
mse = mean_squared_error(y, predictions)
print("Predictions:", predictions)
print("Mean Squared Error:", mse)
Predictions: [48.94736842 60.52631579 72.10526316 83.68421053 89.47368421 95.26315789]
Mean Squared Error: 1.3157894736842093
The Mean Squared Error (MSE) is calculated between the actual final scores and the predicted final scores based only on attendance. The predictions are close but consistently off due to underfitting (because “study_hours” was excluded).
# Plot
import matplotlib.pyplot as plt
plt.scatter(df['attendance'], y, color='blue', label='Actual Scores')
plt.plot(df['attendance'], predictions, color='red', label='Underfit Model')
plt.xlabel('Attendance (%)')
plt.ylabel('Final Score')
plt.title('Underfitting Example: Ignoring Key Features')
plt.legend()
plt.show()
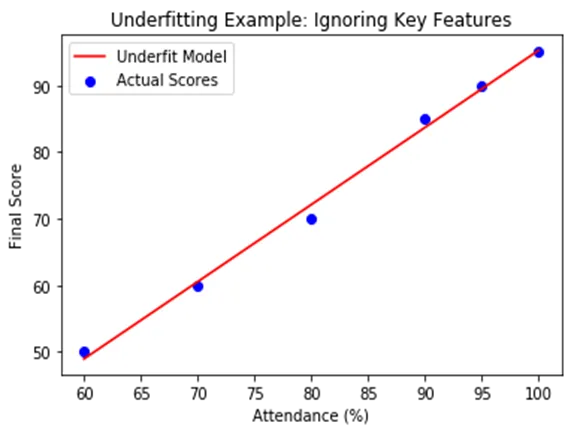
This graph shows us that as attendance increases, the final score also increases — this positive correlation is captured by the regression line. The line does not perfectly follow all the points, especially for high attendance (e.g., 90–100%), where students actually perform better than the model predicts. This shows that the model misses some important information — likely due to ignoring the study_hours.
Underfitting can arise due to several factors:
- Overly Simple Model: Employing an excessively simplistic model — such as a linear regression for a problem with nonlinear relationships — can result in the model failing to learn the true patterns in the data.
- Too Few Features: Excluding relevant variables or relying on a minimal set of features can cause the model to overlook important relationships, leading to poor predictive performance.
- Over-Regularization: Applying strong regularization constraints (like high L1 or L2 penalties) may oversimplify the model, suppressing meaningful patterns in the data.
- Inadequate Model Capacity: Using models with insufficient parameters or shallow architectures may prevent the capture of complex interactions within the dataset, resulting in consistently inaccurate predictions.
The repercussions of underfitting encompass:
- Poor Training and Test Performance: Underfitted models perform inadequately not only on unseen data but also on the training set, indicating a failure to capture the underlying patterns.
- Oversimplification: By using overly simplistic assumptions, underfitted models fail to learn meaningful relationships, resulting in consistently inaccurate predictions.
- Bias Dominance: High bias in the model leads to systematic errors, as it cannot adapt to the complexity of the data, making it ineffective across varying datasets.
- Limited Practical Use: Underfitted models often lack the capacity to provide actionable insights due to their simplistic nature, thereby reducing their effectiveness in real-world applications.
Researchers have responded to the challenge of underfitting by developing a range of techniques aimed at enhancing model learning capacity. Early algorithms such as linear regression and shallow decision trees often suffered from underfitting, particularly when applied to complex datasets with nonlinear relationships. Decision trees, when overly constrained by parameters like shallow depth or high minimum samples per leaf, can become too simplistic to model the intricacies of the data. Techniques such as increasing tree depth, reducing regularization, or expanding feature space can help these models capture more complex patterns. Allowing deeper splits or using ensemble methods like boosting can also significantly reduce underfitting in tree-based models. In the context of neural networks, underfitting may occur when architectures are too small, training time is too short, or regularization is too aggressive. To address this, researchers increase the number of layers or neurons, extend training epochs, or reduce dropout rates. Likewise, in regression tasks, simple models may be insufficient to capture complex data dynamics. In such cases, polynomial regression or feature engineering can help the model learn more nuanced patterns.
Regularization techniques must be used judiciously; excessive regularization in models like lasso or ridge regression can suppress meaningful features and exacerbate underfitting. A careful balance is needed — modifying the regularization parameter (e.g., lowering alpha in ridge regression) allows the model to better adapt to the data. Cross-validation also plays a key role in identifying underfitting by consistently low performance across both training and validation datasets.
To conclude, underfitting results from models being too constrained or simplistic to learn from the data. Effective machine learning models must strike a balance between generalization and learning depth. When a model fails to capture essential trends and performs poorly even on training data, it signals underfitting. Contributing factors include overly simplified model structures, insufficient training duration, excessive regularization, and omission of relevant features. Addressing underfitting involves strategies such as increasing model complexity, adding informative features, relaxing regularization, and ensuring adequate training time. In the future, I hope to demonstrate code examples that help identify and resolve underfitting in practice.
At New Math Data we do all sorts of work in the data science and machine learning space. Please reach out or comment below if you would like to discuss this topic or something adjacent!

